Linear equation들로 이루어진 linear system, 이를 matrix 형태로 표현하는 것, vector, vector들의 linear combination, 그리고 matrix-vector 곱하기 Ax를 A의 column들의 linear combination 형태로 해석하기, x를 매트릭스 A로 linear transform해 새로운 vector Ax를 만들기와 같이 scalar, vector, matrix로 된 식을 적절하게 해석하는데 익숙해져야 linear 식이 얘기하는 것을 들을 수 있다.
Linear System
- The coefficients are also said 'weights'
A system of linear equations (simply, linear system) is a finite set of linear equations, each with the same variables.
ex)
Echelon form of a matrix :
where,
■ : Any nonzero value (pivot). The corresponding column where a pivot is located is a pivot column
* : Any value (including zero)
basic variables : the variables corresponding to pivot columns. In the first matrix above they are x1 and x2
free variables : the variables that are not basic variables. The free variables for the solution of linear system can take on any values (including zero). x3 is the free variable for the example above
Reduced Echelon form : the leading entries are 1's. There are 0's above and below each leading entries.
* A nonzero matrix may be reduced to many echelon forms, but it can have only one unique reduced echelon form
Existence and Uniqueness of Solution for Linear systems
A linear system is consistent if and only if the rightmost column of the augmented matrix is not a pivot column—that is, if and only if an echelon form of the augmented matrix has no row of the form
[0 0 . . . . 0 b ] where b nonzero
If a linear system is consistent, then the system has i) a unique solution when there are no free variables, or ii) infinitely many solutions when there is at least one free variable
Linear Combination of Vectors
A vector that is a sum of scalar multiples of other vectors is called a linear combination of those vectors.
example:
A system of linear equations may now be viewed in three different but equivalent ways: as a matrix equation(4), as a vector equation(5), or as a system of linear equations.
■ The matrix equation Ax =b has a solution if and only if b is a linear combination of the columns of A

A system of linear equations Ax = b (b≠0) with real coefficients has either,
1) a unique solution (a consistent system)
2) infinitely many solutions (a consistent system)
3) no solution (inconsistent system)
* System of linear equations 참고 (* free variable 이 있으면 infinitely many solutions)
* Consistent and inconsistent equations 참고 : System of (Non-homogeneous) linear equations 에서 방정식의 개수와 미지수 개수를 갖고는 system of equation이 consistent(해가 있을 지) 또는 inconsistent(해가 없을 지) 판단할 수 없다. 보통 augmented matrix를 Gaussian elimination해서 "5 = -1" 같은 false statement가 유도되어 solution이 없음을 알던가, 또는 free variable이 보여 infinitely many solution이 있음을 판단.
■ Homogeneous Linear Systems
A system of linear equations is homogeneous if it can be written as Ax = 0, where A is an m x n matrix and the 0 is zero vector in Rm.
An homogeneous system of linear equations Ax = 0 cannot have no solution (ie. Homogeneous system은 최소한 하나의 솔루션 x = 0을 갖고 있어 consistent. It can have one unique solution, x = 0 also called trivial solution or infinitely many solutions). For a given equation Ax = 0, the important question is whether there exists a nontrivial solution.
In a homogeneous system of equations of m linear equations and n variables, where m < n, the system has infinitely many solutions.
위의 Existence and Uniqueness of Solution for Linear systems 에서 consistent한 linear system에서 free variable이 없으면 하나의 유일한 솔루션만 있다고 했으니, 이 경우 homogeneous system은 x = 0 이 되며, 따라서 homogeneous system 이 non-trivial 한 솔루션을 가지려면 free variable이 있어야 하겠다.
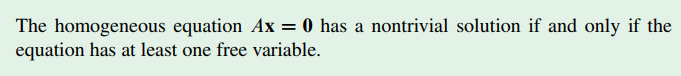
■ Linear Independence

Linear Independence/dependence를 matrix equation 형태로 나타내면,

역시, Ax = 0 의 augmented matrix 에서 free variable이 없어야 A matrix의 column들이 independent.
■ Linear Transformation
Ax = b (where, A가 m × n matrix, x는 Rn 벡터) 같이 matrix - vector multiplication 행렬식을 행렬 A로 x를 벡터 b (b 는 Rm)로 변환하는 Matrix Transformation (mapping) 이라 말한다. 모든 Matrix Transformation은 Linear Transformation.
Ax = b 의 해를 구함은 Linear transformation matrix (operator) A로 인해 b로 될 수 있는 모든 x를 구한다는 것과 같은 뜻.
아래에서
transformation T가 모든 scalar c와 vector v에 대해 아래 식을 만족하면 T는 linear transformation.
'Learning & Reasoning > Math Revisit' 카테고리의 다른 글
| Eigenvalues and Eigenvectors (고유값과 고유벡터) (0) | 2016.03.28 |
|---|---|
| Determinants (0) | 2016.03.24 |
| Vector Spaces (0) | 2016.03.21 |
| 행렬 (0) | 2016.03.17 |
| Expectation, Variance, Covariance 공식 (0) | 2016.01.03 |













